Regression discontinuity with sci-kit learn models

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import ExpSineSquared, WhiteKernel
from sklearn.linear_model import LinearRegression

import causalpy as cp

WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.

%config InlineBackend.figure_format = 'retina'

Load data

data = cp.load_data("rd")
data.head()

	x	y	treated
0	-0.932739	-0.091919	False
1	-0.930778	-0.382663	False
2	-0.929110	-0.181786	False
3	-0.907419	-0.288245	False
4	-0.882469	-0.420811	False

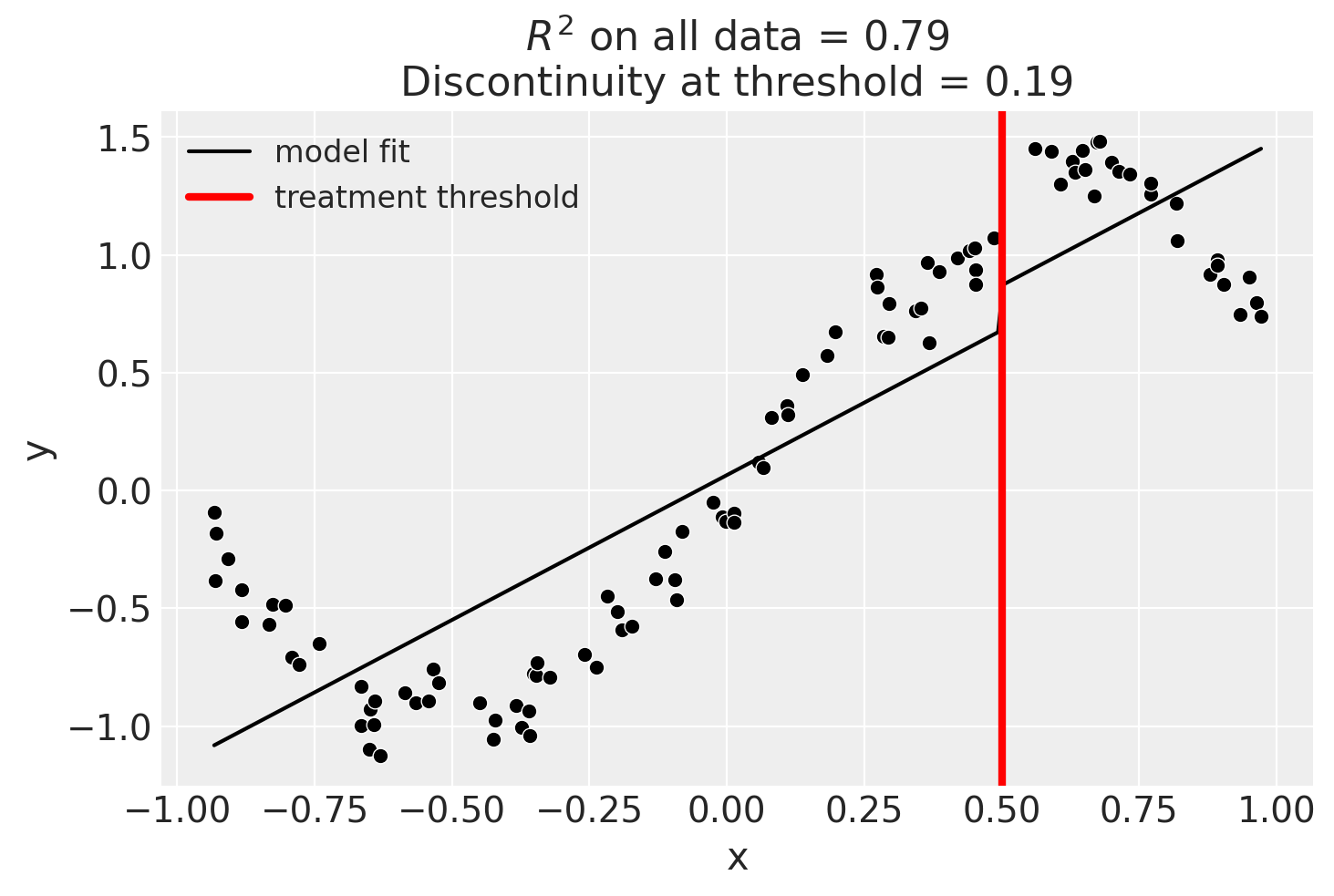
Linear, main-effects model

result = cp.skl_experiments.RegressionDiscontinuity(
    data,
    formula="y ~ 1 + x + treated",
    model=LinearRegression(),
    treatment_threshold=0.5,
)

fig, ax = result.plot();

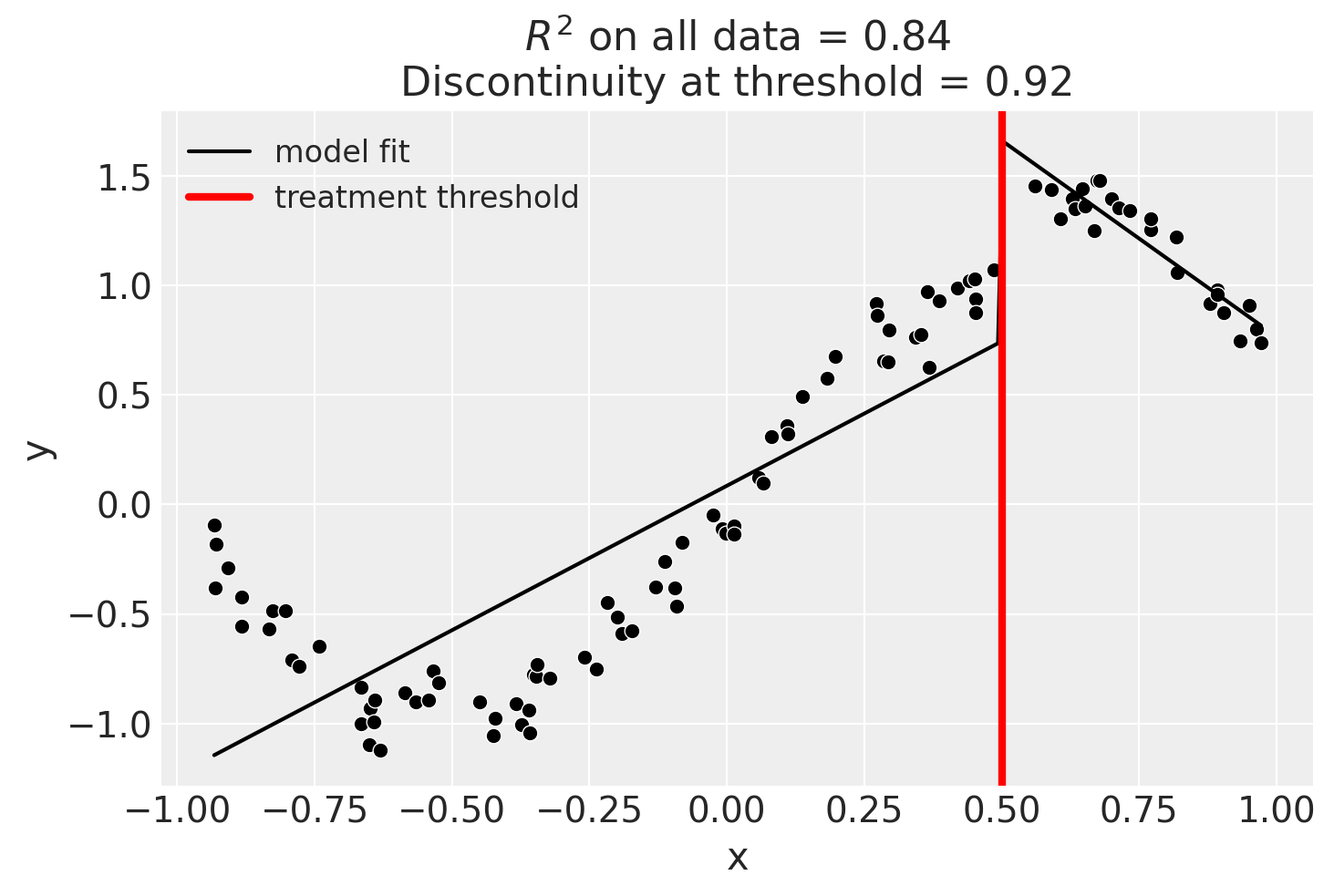
Linear, main-effects, and interaction model

result = cp.skl_experiments.RegressionDiscontinuity(
    data,
    formula="y ~ 1 + x + treated + x:treated",
    model=LinearRegression(),
    treatment_threshold=0.5,
)

result.plot();

Though we can see that this does not give a good fit of the data almost certainly overestimates the discontinuity at threshold.

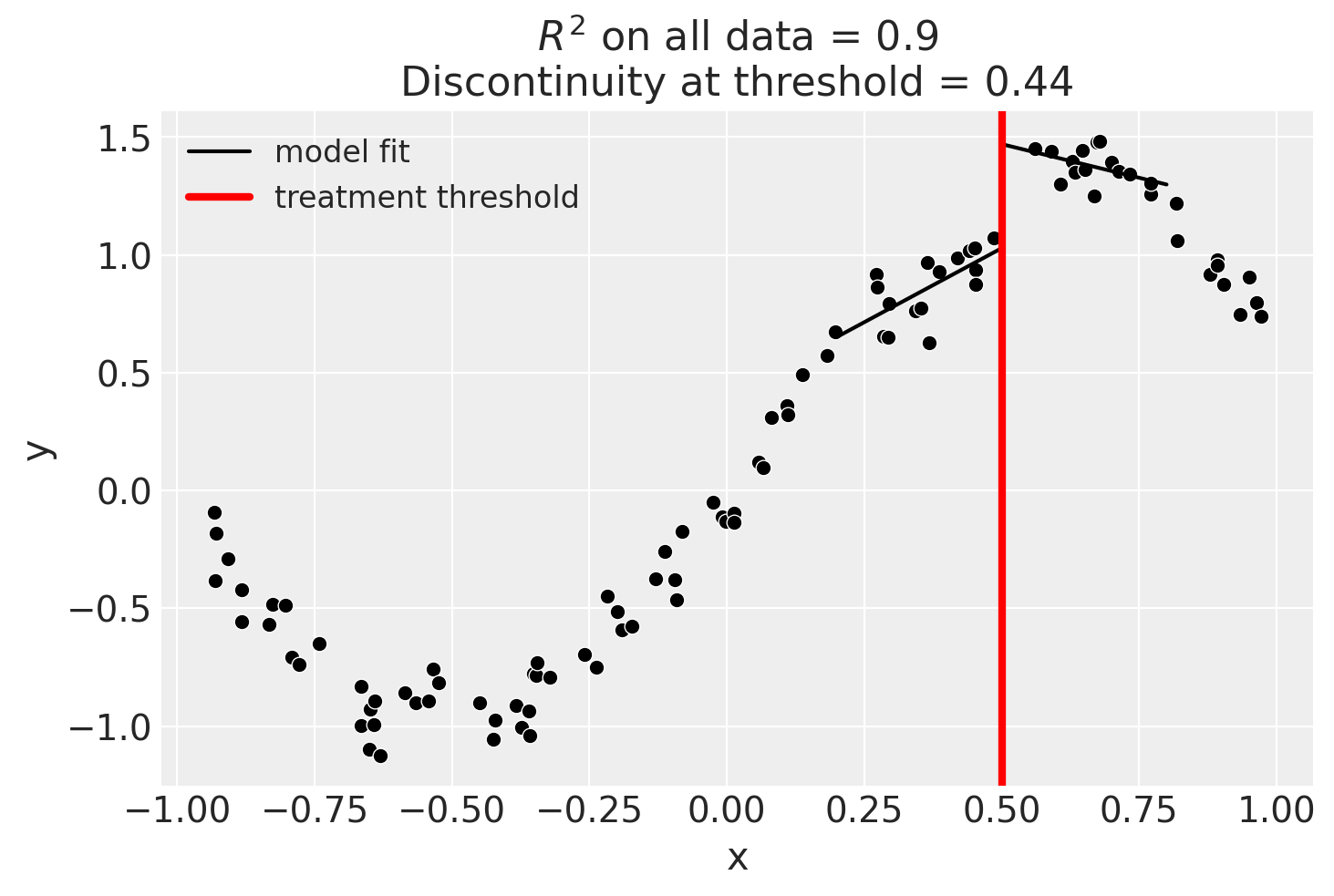
Using a bandwidth

One way how we could deal with this is to use the bandwidth kwarg. This will only fit the model to data within a certain bandwidth of the threshold. If \(x\) is the running variable, then the model will only be fitted to data where \(threshold - bandwidth \le x \le threshold + bandwidth\).

result = cp.skl_experiments.RegressionDiscontinuity(
    data,
    formula="y ~ 1 + x + treated + x:treated",
    model=LinearRegression(),
    treatment_threshold=0.5,
    bandwidth=0.3,
)

result.plot();

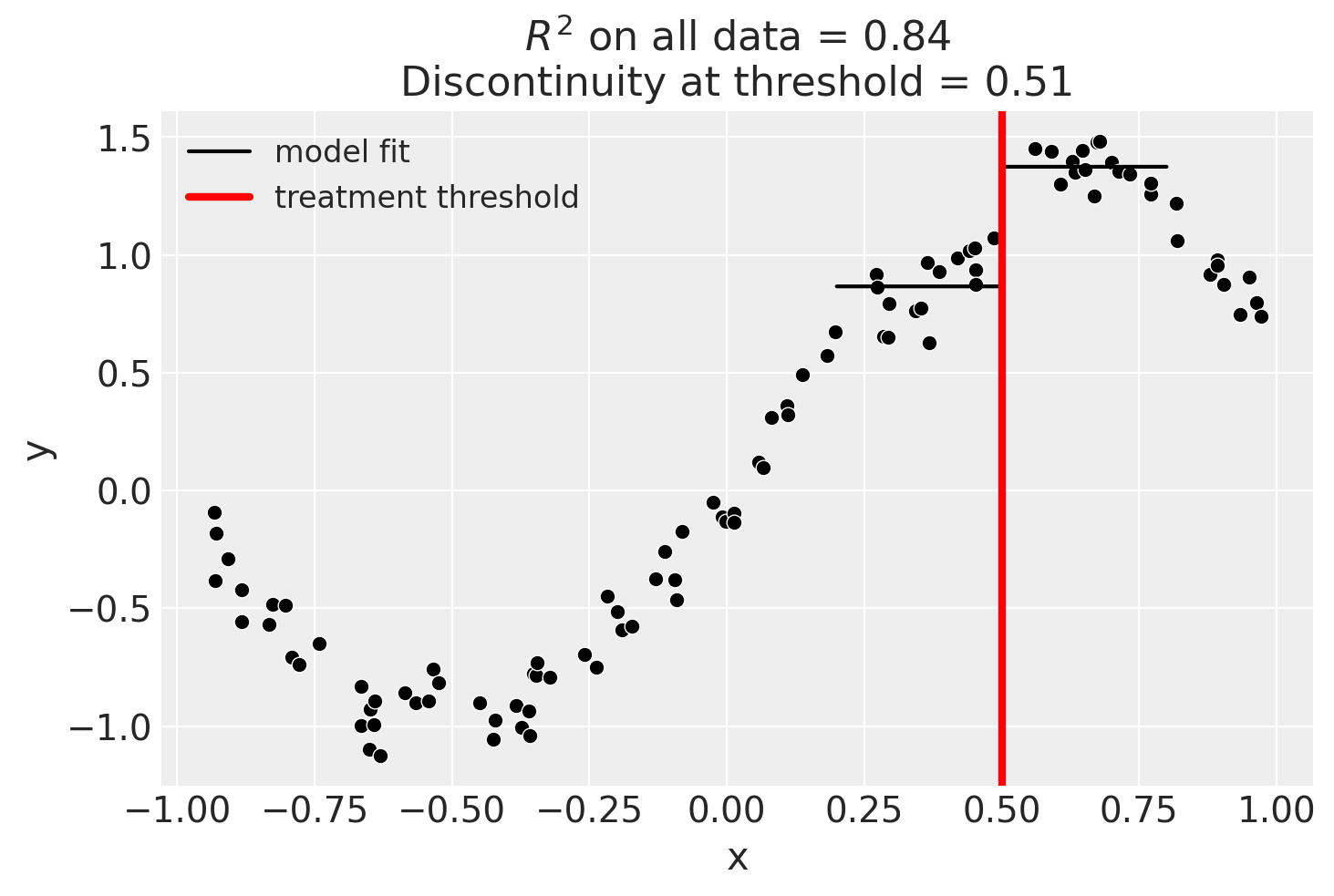
We could even go crazy and just fit intercepts for the data close to the threshold. But clearly this will involve more estimation error as we are using less data.

result = cp.skl_experiments.RegressionDiscontinuity(
    data,
    formula="y ~ 1 + treated",
    model=LinearRegression(),
    treatment_threshold=0.5,
    bandwidth=0.3,
)

result.plot();

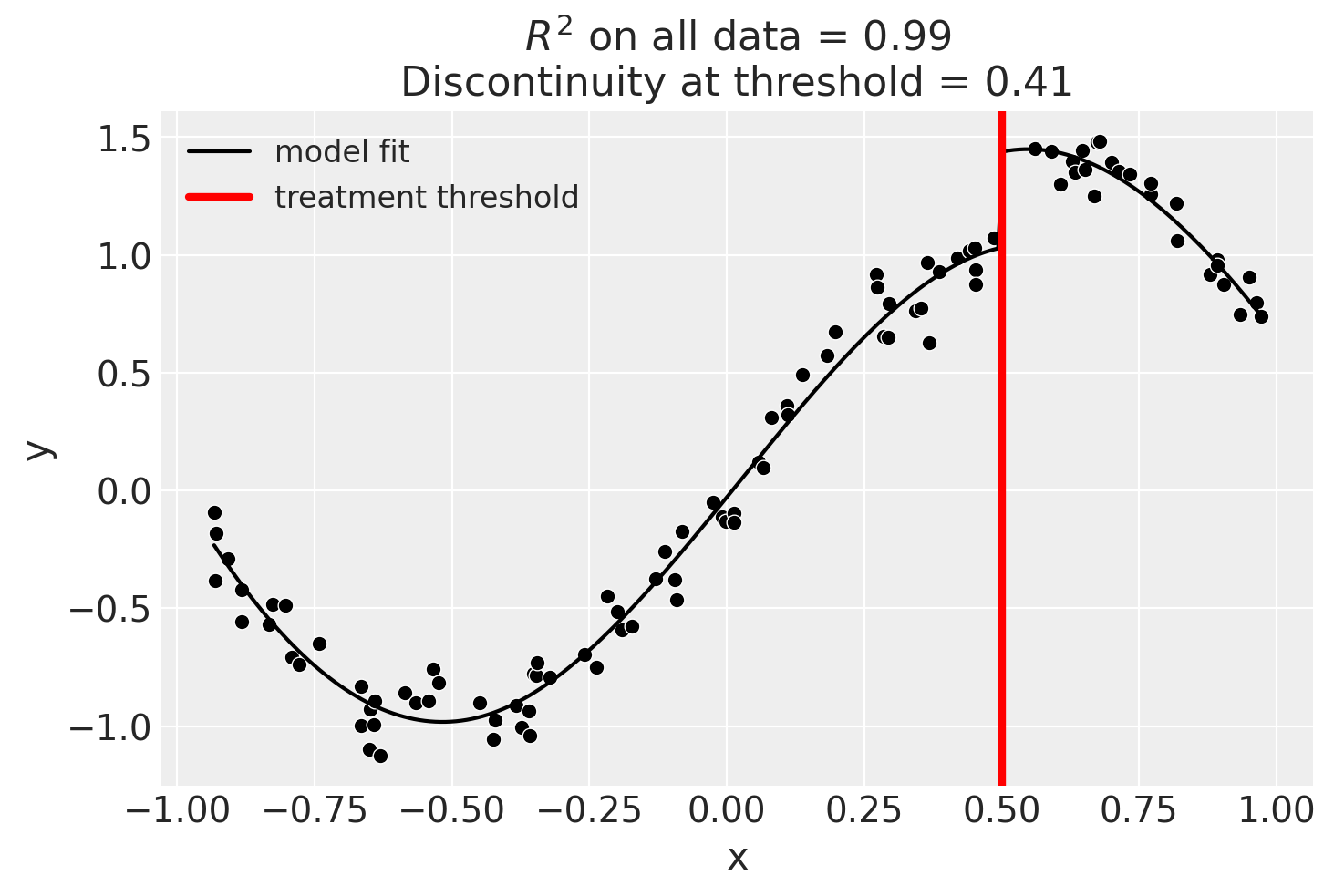
Using Gaussian Processes

kernel = 1.0 * ExpSineSquared(1.0, 5.0) + WhiteKernel(1e-1)
result = cp.skl_experiments.RegressionDiscontinuity(
    data,
    formula="y ~ 1 + x + treated",
    model=GaussianProcessRegressor(kernel=kernel),
    treatment_threshold=0.5,
)

fig, ax = result.plot();

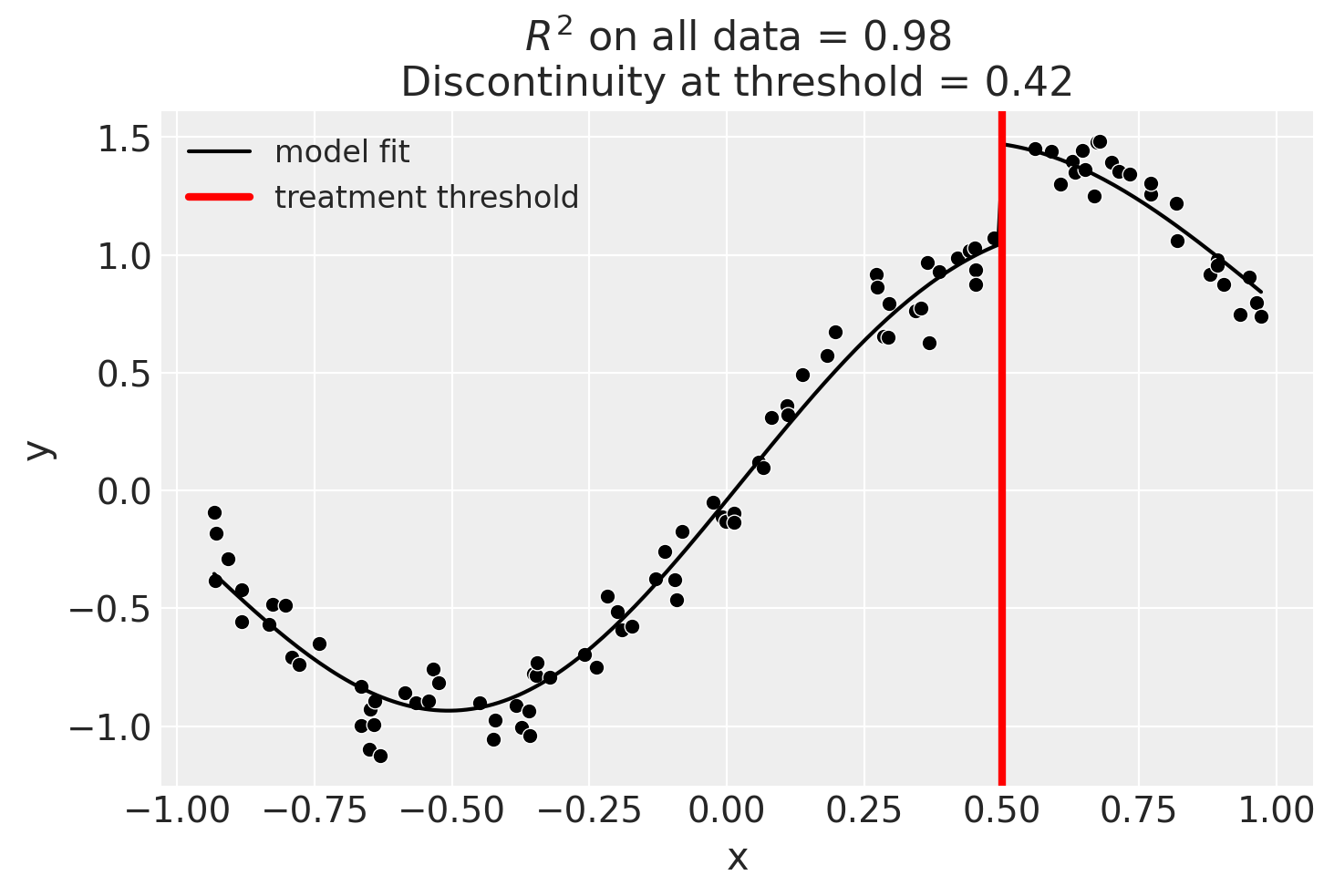
Using basis splines

result = cp.skl_experiments.RegressionDiscontinuity(
    data,
    formula="y ~ 1 + bs(x, df=6) + treated",
    model=LinearRegression(),
    treatment_threshold=0.5,
)

fig, ax = result.plot()