Synthetic control with sci-kit learn models

from sklearn.linear_model import LinearRegression

import causalpy as cp

Load data

df = cp.load_data("sc")
treatment_time = 70

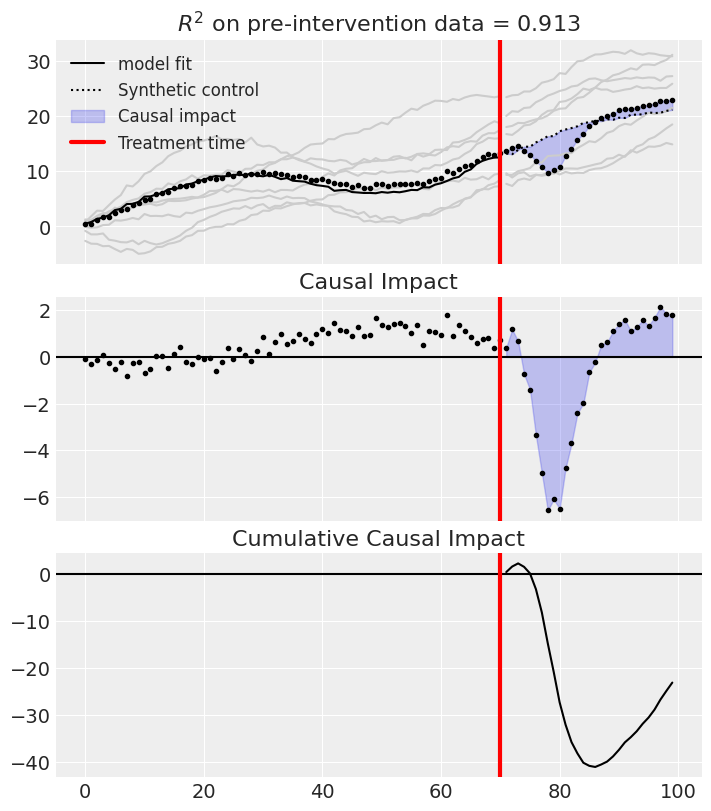
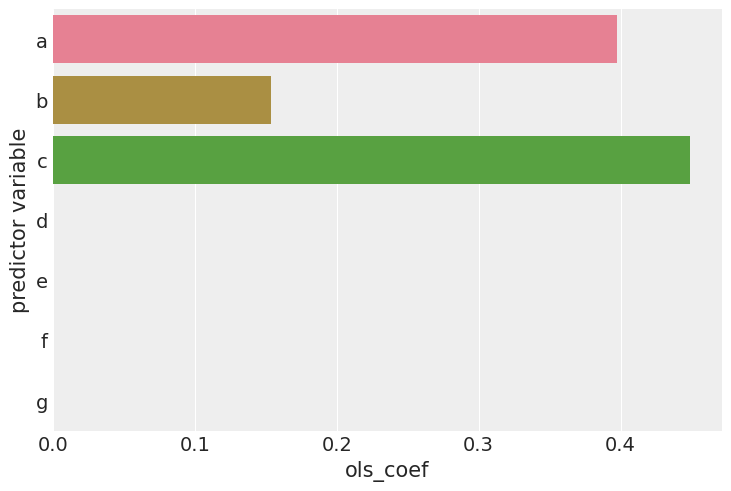
Analyse with WeightedProportion model

# Note, we do not want an intercept in this model
result = cp.skl_experiments.SyntheticControl(
    df,
    treatment_time,
    formula="actual ~ 0 + a + b + c + d + e + f + g",
    model=cp.skl_models.WeightedProportion(),
)

fig, ax = result.plot(plot_predictors=True)
../_images/9ddfb627674f02ce5286d8d8348f2a8dbf9618c3e7e9d49f75b8ca0cc6f16d03.png 
result.plot_coeffs()
../_images/126dd62f21fe1dbfd65591ea78c3d8a6142948758f0d2d6ae5f6cf49fe1cf334.png

But we can see that (for this dataset) these estimates are quite bad. So we can lift the “sum to 1” assumption and instead use the LinearRegression model, but still constrain weights to be positive. Equally, you could experiment with the Ridge model (e.g. Ridge(positive=True, alpha=100)).

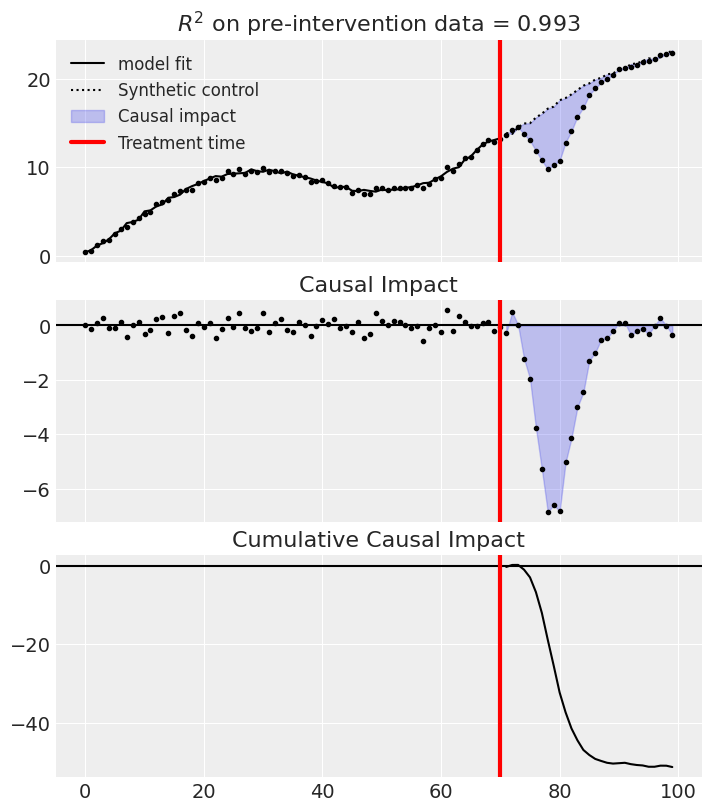
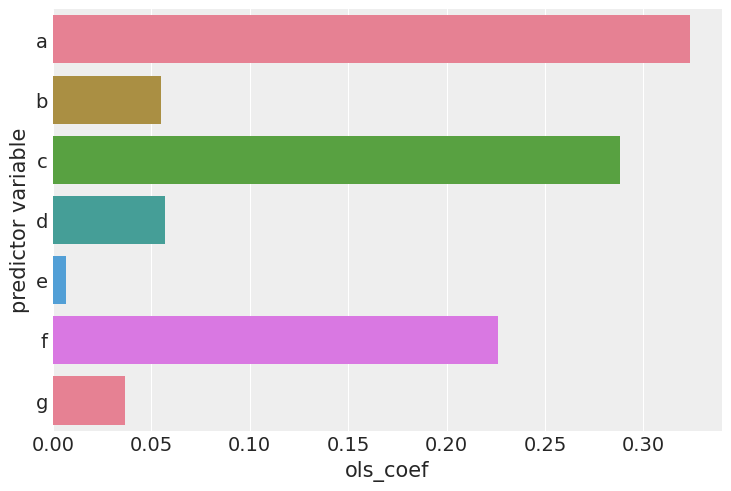
Analyse with the LinearRegression model

# Note, we do not want an intercept in this model
result = cp.skl_experiments.SyntheticControl(
    df,
    treatment_time,
    formula="actual ~ 0 + a + b + c + d + e + f + g",
    model=LinearRegression(positive=True),
)

fig, ax = result.plot()
../_images/c5a57f41ce3cf272e799654e1d22ceca03c1b91cda77aa256e1cd88602c41712.png 
result.plot_coeffs()
../_images/a0dacc27cf7a89233b65ce89acaa19c1bec1251e08ddd621d799dcf0033379e9.png